Домашнее задание на 15.05

 

Домашнее задание

По желанию. Для тех, кто хочет улучшить свои оценки. Прислать учителю информатики до 15.05.2021  до 23.00 по школьной эл почте письмо-отчет о выполнении домашнего задания. Задание находится ЗДЕСЬ.

Урок 27. Поиск минимума и максимума в массиве. Теория

 Дата проведения занятия 19.04.21 

ПОСЛЕДОВАТЕЛЬНЫЙ ПОИСК В МАССИВЕ

В программировании поиск - одна из наиболее часто встречающихся задач невычислительного характера.

Предположим, что в некотором массиве хранятся результаты забега на 100 метров.

• Необходимо выяснить, кто занял первое место.
• Необходимо выяснить, кто занял 1, 2, 3 место
• Необходимо выяснить, насколько победитель пробежал быстрее самого слабого участника 

Все эти задачи сводятся к поиску максимального и   минимального значения элемента массива
Компьютер не может сравнить разом весь ряд объектов. На каждом шаге он может сравнивать только два объекта. Поэтому в программе необходимо организовать последовательный просмотр элементов массива и сравнение значения очередного просматриваемого элемента с некоторым образцом

Пример программы поиска первого минимума
Пример программы поиска последнего максимума

Работа на ПК в классе:

Выполните в классе задание на поиск экстремумов

Вариант 1 для 9а, Вариант 2 для 9б,  Вариант 3 для 9в 

Урок 26. Решение задач с циклами

 Дата проведения занятия 12.04.21

Работа на ПК в классе:

 Вариант 1, 2 для 9а, 9б; Вариант 3, 4 для 9в 

Задачи с сайта К. Полякова

polyakov-15-3. Напишите программу, которая в последовательности натуральных чисел определяет сумму всех чисел, кратных 7 и оканчивающихся на 2. Программа получает на вход натуральные числа, количество введённых чисел неизвестно, последовательность чисел заканчивается числом 0 (0 – признак окончания ввода, не входит в последовательность). Количество чисел не превышает 1000. Введённые числа не превышают 30 000. Программа должна вывести одно число: сумму всех чисел, кратных 7 и оканчивающихся на 2.
Пример работы программы:

polyakov-15-4. Напишите программу, которая в последовательности целых чисел определяет количество чётных чисел, кратных 7. Программа

получает на вход целые числа, количество введённых чисел неизвестно, последовательность чисел заканчивается числом 0 (0 – признак окончания ввода, не входит в последовательность). Количество чисел не превышает 1000. Введённые числа по модулю не превышают 30 000. Программа должна вывести одно число: количество чётных чисел, кратных 7.
Пример работы программы:

polyakov-15-5. Напишите программу, которая в последовательности натуральных чисел находит среднее арифметическое трёхзначных чисел или сообщает, что таких чисел нет (выводит NO). Программа получает на вход натуральные числа, количество введённых чисел неизвестно, последовательность чисел заканчивается числом 0 (0 – признак окончания ввода, не входит в последовательность). Количество чисел не превышает 100. Введённые числа не превышают 300. Программа должна вывести среднее арифметическое трёхзначных чисел или вывести NO, если таких чисел нет.

Пример работы программы:

Цикл FOR и случайные числа

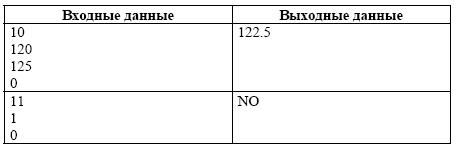
 Дата проведения занятия 5.04.21

ЦИКЛ FOR -  ЦИКЛ С ЗАДАННЫМ ЧИСЛОМ ПОВТОРЕНИЙ, ЦИКЛ С ПАРАМЕТРОМ

Оператор цикла for имеет одну из двух форм:

for var переменная: тип := начальное значение to конечное значение do
  оператор

или

for var переменная: тип := начальное значение downto конечное значение do
  оператор

Текст от слова for до слова do включительно называется заголовком цикла, а оператор после do - телом цикла. Переменная после слова for называется параметром цикла.
Для первой формы цикла с ключевым словом to параметр цикла меняется от начального значения до конечного значения, увеличиваясь всякий раз на единицу, а для второй формы с ключевым словом downto - уменьшаясь на единицу.
Для каждого значения переменной-параметра выполняется тело цикла. Однократное повторение тела цикла называется итерацией цикла. Значение параметра цикла после завершения цикла считается неопределенным.

Если для цикла for ... to начальное значение переменной цикла больше конечного значения или для цикла for ... downto начальное значение переменной цикла меньше конечного значения, то тело цикла не выполнится ни разу.

Изменение переменной-параметра цикла внутри цикла является логической ошибкой.

ЗАПОЛНЕНИЕ МАССИВА

Цикл for ... to или for ... downto удобно использовать для работы с массивами: для заполнения, для поиска элементов с заданными свойствами.
1. Заполнение массива из 10 элементов вводом значений с клавиатуры
    for var i:=10 downto 1 do read ( a[i] ); // заполнение от 10 элемента до 1
2. Заполнение массива из 10 элементов с помощью оператора присваивания
     for var i:=1 to 10 do a[i]:=i+2; // заполнение от 1 элемента до 10

3. Заполнение массива из 10 элементов случайными числами
     randomize; // активизация датчика случайных чисел
     for var i:=1 to 10 do a[i]:=random(50, 100); // каждый элемент - случайное число [ 50;100]

     for var i:=1 to 10 do a[i]:=random(100); // каждый элемент - случайное число [ 0;100)

Работа на ПК в классе:

 Вариант 1, 2 для 9а, 9б; Вариант 3, 4 для 9в 

Домашнее задание

Прислать учителю информатики до 10.04.21  до 23.00 по школьной эл почте письмо-отчет о выполнении домашнего задания. Задание находится ЗДЕСЬ-9pas6-hm21.

Урок 24. Массивы

 Дата проведения занятия 28.03.21

До сих пор в Паскале вы имели дело с простыми типами данных. К простым типам относятся порядковые (целые, логические, символьные)  и вещественные типы данных

Сегодня мы переходим к изучению массивов. Массивы относятся к  структурированным типам данных.

Массив представляет собой набор элементов одного типа, каждый из которых имеет свой номер, называемый индексом (индексов может быть несколько, тогда массив называется многомерным). Индекс определяет положение элемента в массиве.

Перед использованием в программе массив должен быть описан, то есть должно быть указано имя массива, количество элементов и их тип. Это необходимо для того, чтобы выделить участок памяти нужного размера для хранения элементов массива. Общий вид описания массива:
var  <имя_массива>: array [<мин_зн_индекса> .. <макс_зн_индекса>] of <тип_элементов>;
Тип индекса обязательно представляет собой интервальный тип и обязательно должен задаваться в виде a..b, где a и b - константные выражения целого, символьного или перечислимого типа.
Например, массивы a1,a2 состоят каждый из 10 целочисленных элементов, а массив b состоит из 6 вещественных чисел:

var
  a1,a2: array [1..10] of integer;
  b: array [0 .. 5] of real;

В программе к элементу массива a1 с номером i следует обращаться так: a1[i]

Переменные-массивы одного типа можно присваивать друг другу, при этом будет производиться копирование содержимого одного массива в другой:

a1:=a2;

Пример программы с массивом

В качестве примера напишем программу Pas20_0_cl.pas по следующему заданию:

Заполнить массив из 10 элементов целыми  числами от 3 до 12.
Массив объявлен как var arr00: array [1..10] of  integer. Вывести значения элементов массива на экран в одну строку через знаки  ; . Сосчитать сумму элементов,  вывести сумму на экран с новой строки.

Работа на ПК в классе:

1. Отладить программу  Pas20_0_cl.pas, показать учителю (для всех)
2. Далее работаем по вариантам Вариант 1, 2 для 9а, 9в;   Вариант 3, 4 для 9б

Домашнее задание

Прислать учителю информатики до 3.04.21 до 23.00 по школьной эл почте письмо-отчет о выполнении домашнего задания. Задание находится ЗДЕСЬ-9pas4-hm20.

Урок 23. Оператор цикла WHILE

 Дата проведения занятия 15.03.21

ОПЕРАТОР WHILE - ЦИКЛ С УСЛОВИЕМ

Синтаксис (справка по Паскалю, цикл с условием)
Оператор цикла while имеет следующую форму:

while условие do
  оператор

Условие представляет собой выражение логического типа, а оператор после do называется телом цикла. Перед каждой итерацией цикла условие вычисляется, и если оно истинно, то выполняется тело цикла, в противном случае происходит выход из цикла.
Если вместо одного оператора в теле цикла требуется выполнить несколько операторов, то используется блок команд begin...end.
Если условие всегда оказывается истинным, то может произойти зацикливание:

while 2>1 do
    write(1);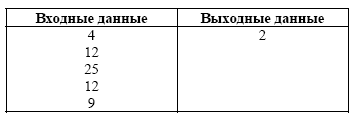

Чтобы прервать зациклившуюся программу, выполняющуюся из интегрированной среды в режиме связи с оболочкой, следует использовать комбинацию клавиш Ctrl-F2 или пункт меню Программа/Завершить

Работа на ПК в классе:

Правила оформления программы

1. Программу следует  начать с комментария, в котором содержится условие задачи и набор тестовых данных. Тестовые данные — это те данные, на которых надо проверять работу программы
2. Программу следует отформатировать (кнопка 4 справа)
3. Программу следует сопровождать комментариями по тексту
4. Программу следует начать с приветствия

writeln ('Вас приветствует программа Петрова П');

Варианты назначает учитель

Вариант 1: Выполнить  While7, While14, сохранить в своей папке Pascal  на локальном диске  

Вариант 2: Выполнить  While8, While13, сохранить в своей папке Pascal  на локальном диске 

Вариант 3: Выполнить  задачи с сайта К. Полякова, сохранить в своей папке Pascal  на локальном диске

polyakov-15-1. Напишите программу, которая в последовательности натуральных чисел определяет количество чисел, кратных 3 и оканчивающихся на 2. Программа получает на вход количество чисел в последовательности, а затем сами числа.
Количество чисел не превышает 1000. Введённые числа по модулю не превышают 30 000. Программа должна вывести одно число: количество чисел, кратных 3 и оканчивающихся на 2.
Пример работы программы:

polyakov-15-2.Напишите программу, которая в последовательности натуральных чисел определяет сумму всех чисел, кратных 6 и оканчивающихся на 4. Программа получает на вход натуральные числа, количество введённых чисел неизвестно, последовательность чисел заканчивается числом 0 (0 – признак окончания ввода, не входит в последовательность). Количество чисел не превышает 1000. Введённые числа не превышают 30 000. Программа должна вывести одно число: сумму всех чисел, кратных 6 и оканчивающихся на 4.

Пример работы программы:

Урок 21. Повторение. Типы данных. Арифметические операции

 Дата проведения занятия 1.03.21

Итак, переменная - это величина, которая  имеет ИМЯ, ТИП, ЗНАЧЕНИЕ
Теорию законспектировать дома

1. Имя переменной

В именах МОЖНО использовать:

• латинские буквы (A - Z), причем строчные и заглавные буквы в Паскале не различаются
• цифры (0 - 9), имя не может начинаться с цифры
• знак подчеркивания _

В именах НЕЛЬЗЯ использовать:

• русские буквы
• пробелы
• скобки, знаки +, =, !, ? и др

2. Тип данных (тип переменной)

Основными числовыми типами данных в Паскале являются

• integer (синонимом является longint) - целый 
• real (синонимом является double) - вещественный
• boolean - логический

 3. Переменную нужно объявить в программе для выделения под нее памяти 

var a, b, c: integer; // целые a, b, c
var d, f: real;          // вещественные d, f
var log: boolean;    // логический

4. Присвоить значение переменной - значит записать новое значение в переменную. Знак присвоения :=

a:=6;   d:=a; d:= d + 5;
5. Арифметические операции
Над числовыми данными выполняются следующие операции:
*  (умножение) для integer, real;
/   (деление) для integer, real;
div (получение целого частного) только  для integer;
mod (получение целого остатка деления) только  для integer.
+  (сложение) для integer, real;
-   (вычитание) для integer, real;
Подробнее про арифметические операции читать здесь

Порядок выполнения операций:

• вычисление выражений в скобках 
• умножение, деление, div, mod слева направо 
• сложение и вычитание слева направо

Работа на ПК

Задание 1
1. Напишите в тетради программу Pas9_cl_05_name, которая вводит 2 целых числа x, y, последовательно считает:

• сумму, выводит результат на экран
• произведение, выводит результат на экран
• среднее арифметическое x и y, выводит результат на экран
• остаток от деления x на 2, выводит результат на экран
• последнюю цифру y, выводит результат на экран
• результат сравнения y > 10, выводит результат на экран

2. Наберите текст программы в окне Паскаля

3. Отформатируйте текст, нажав на 4-ую справа кнопку в меню окна PascalABC.NET
4. Сохраните текст программы на локальном компьютере в своей папке, во вложенной папке Pascal_name под именем Pas9_cl_05_name.pas
5. Сделайте компиляцию программы (Ctrl + F9).
6. Если нет синтаксических ошибок, то запустите программу (F9) 3 раза с разными данными
7. Проанализируйте полученный результат

Задание 2
Напишите программу Begin 32 - перевод градусов по С в градусы по F

Задание 3
Напишите программу Integer7: Дано двузначное число. Найти сумму и произведение его цифр.

Домашнее задание

Задание 0 - законспектировать теорию

Задание 1
Доделать программу Pas9_cl_05_name из классного Задания 1
Задание 2

1. Написать в тетради программу вычисления площади прямоугольного треугольника S по двум катетам a, b. Значения a и b - это исходные данные, их требуется ввести, S - результат работы программы, его требуется вывести
2. Набрать на ПК. Дать имя программе  pas9_hm_03_name (name - фамилия автора программы)
3. Сохранить файл под именем Pas9_hm_03_name.pas
4. Запустить программу в среде PascalABC.Net
5. Сделать сканирование экрана ( кнопка Print Screen)

Задание 3
Написать программу  Begin 35 или  Integer7 (Дано двузначное число. Найти сумму и произведение его цифр.)

Прислать учителю информатики до 13.03.21 до 22.00 по школьной эл почте письмо-отчет о выполнении домашнего задания.
Тема письма: 9 кл ДЗ к уроку Паскаль-2 <ваша фамилия>

К письму прикрепить по 2 файла для каждой решенной задачи: скриншот экрана с результатом выполнения программы и свой файл типа .pas,

Если что-то не получилось, в письме написать причину невыполнения задания